an ideal gas has no energy at all
a real gas will have some energy, (due to it's mass), the zero point energy
A Reversible process is
a process which can be made to go in the reverse direction by an infinitesimal change in the conditions which are causing it took take place.
is defined as the amount of energy required to break bonds. L is the DQ you need to put into a system in order to melt/vaporise it. It goes into both DU and DW. The material will expand or contract due to the change, so DW ¹ 0. DU ¹ 0 either, because the internal potential energy will increase as well (not the internal kinetic energy though).
Specific latent heat of fusion (l)
The heat of fusion per unit mass. Units: J kg-1.
Ideal gas laws apply least at
high pressure
low temperature
(when the gas is close to liquefaction)
Real gases have intermolecular forces and their molecules have volume.
compared CO2 and N2 gases. N2 nearly ideal at the T, p he was using.
--> Volume
Important things about the apparatus:
gases were dry
their volumes could be found for a specific pressure
pressure altered using screws in a water bath
mercury separates water bath from the gases, keeping them dry
Andrews found the pressure of the CO2 from the volume of the N2 - which he assumed to be ideal
He plotted p-V graphs at various fixed temperatures (isothermals)
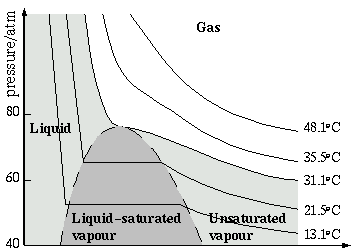
Above the critical temperature Tc (31.1OC for CO2) a substance is always a gas. It is not possible to liquefy it by compression. Below this point a substance can exist as an unsaturated vapour (technical term for a substance in gas phase below Tc), a liquid, or an equilibrium mixture of the two.
The minimum pressure at which a gas can be liquefied at Tc. (This is the top of the darker grey curve).
Specific critical volume
The volume of a gas at it's Tc and pc .
The liquid and it's saturated vapour have the same volume at this point, and so have the same density. There is no meniscus- and therefore no distinction between liquid and vapour.
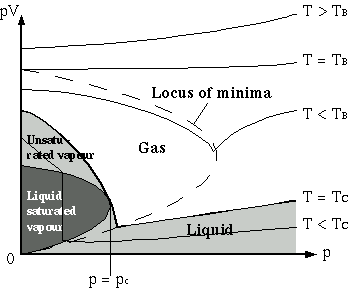
The temperature at which the gas's behaviour is closest to an ideal gas, ie. Increasing p has little (ideally no) effect on pV.
This is TB on the left hand graph of pV against p.
is the process by which a liquid becomes a gas.
Rate of evaporation depends on surface area, temperature, air movement around the surface (the more the better) and air pressure (the lower the better). Evaporation cools a liquid because the molecules with the highest EK are lost first, so average EK drops.
Freon has TC > room temperature, so it can be liquefied at room temperature by compression.
Pump -> cooling fins -> valve -> inside of fridge -> pump.
A temperature change occurs when a gas at one constant pressure is forced through a hole into a region at a constant, lower pressure. The gas expands quickly on reaching the other side: no heat is put in or removed, so this is adiabatic expansion.
For an ideal gas, the internal energy will be used to do work in expanding the gas. But the same amount of work has to be done in forcing the gas through the hole. So, overall, there is no Joule-Kelvin effect for ideal gases.
A real gas gets colder only if it's temperature is already below Ti. Above the inversion temperature, the work done in forcing the gas through the hole is enough to heat it up (work must be done in doing this, as the gas molecules have volume and I/M forces). This can be seen from the pV/p graph: the graph curves upwards for T > TB, and Ti > TB.
The change in temperature depends on the internal energy lost through expansion, and the work done in forcing the gas through the hole.
The inversion temperature Ti takes into account both of these factors. It is the point below which compression will cool the gas. Ti > TB.
Superconductors
Gold, Silver, Copper, and ferric metals do not superconduct.
Other metals, and some ceramics, do superconduct:
below a critical temperature (Tc)
and below a critical B-field strength (Bc)
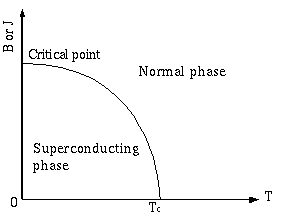
Values of Bc and Jc are found for 0K (maximum).
Superfluids
Helium 4 is a superfluid below 2.17K (the lambda point, Tl) . Below this point it acts like a mixture of two liquids: a normal liquid, and a superfluid. It is called Helium II (instead of Helium I, it's when a liquid name above this point (2.17 to 4.2K)).
The superfluid has no viscosity, so it can flow through capillaries that are too narrow for a gas.
It also conducts heat very well (best known conductor of heat).
At 2.17K (Tl ) there is a marked change in the specific heat capacity of the helium: a graph of specific heat capacity against temperature peaks at this point.
A heating coil will cause the thermomechanical effect to occur: a slight temperature difference will cause the superfluid to flow towards the heat, and this results in the fountain effect.
As the temperature is decreased, the amount of superfluid present increases
Liquid helium 4 can escape from an open-topped container by creeping in the form of a thin film over the walls.
The superfluid has less thermal energy than the normal liquid, and so if it is forced out of the container through a thin capillary, the temperature in the first container will increase.
Helium 3 also becomes a superfluid at about 0.003K
Electrons in a superconductor can be regarded as a superfluid.
9.3 Special Relativity
it was thought that light travelled with a fixed speed relative to the ether
the existence of the ether was considered necessary in order to explain how light travelled through a vacuum
compares speed of light in the direction of the Earth's motion with that at right angles to it
Ways to explain the result
The ether is dragged along by the Earth. The phenomenon of stellar aberration disproves this.
Light always travels at the same speed with respect to it's source. This was rejected because this would make light unique - no other wave motions do this.
Objects moving through the ether with velocity v contract in the direction of their motion by a factor †(1 - v2/c2) - Fitzgerald-Lorentz contraction.
So either
there is no ether
or the ether is undetectable because of Fitzgerald-Lorentz contraction
Both of which leads to the conclusion that
there is no absolute motion
the speed of light is the same in any inertial frame
An inertial frame is one where Newton's First Law is valid.
Law 1: if no resultant force acts on a body, it's velocity will not change.
(F=0, therefore Dv = 0)
Based on two postulates:
Physical laws have the same form in all inertial frames of reference. (the principle of special relativity)
The speed of light (in vacuum) is the same in all inertial frames. It does not depend on the velocity of the source or the observer.
So an experiment performed in one inertial frame will have the same result in any other inertial frame. No one frame is at rest. All motion is relative.
an observer regards a clock in a different inertial frame as running slower than an identical clock in his own inertial frame
Proper time (t0) is the time interval between two events measured in the frame in which they both occur at the same point. It is less than any other measurement of the time interval.
an observer will regard objects moving relative to him as being shorter than they actually are
objects contract in the direction of relative motion
Proper length (L0) is the length of an object measured in that object's inertial frame. It is greater than any other measurement of the object's length.
One observer may perceive a length contraction effect (eg. distance between two points in space is shorter) and another may perceive a time dilation effect (eg. spaceship seems to take longer to move from one point to the other).
Relativistic momentum = mv = m0v / †(1 - v2 / c2 )
Total energy of a body = rest energy + relativistic kinetic energy
total energy is conserved
The rest energy is simply m0c2.
The total energy is mc2.
From these, the relativistic kinetic energy can be found:
K = mc2 - m0c2
When v << c, K = ½m0v2.
For the photon in a box derivation, you need to know
a photon of light energy E has momentum E / c
box recoils on photon emission. It's momentum increases. It drops to zero when the photon hits the other side (totally inelastic)
box has no mass. But the photon source has mass ms.
Use conservation of momentum to work out how the photon mass relates to the photon energy. Comes out as E=mc2.
Confirmation
muon decay
decrease in mass during fission
decay of fundamental particles eg. mesons
9.2 Wave particle duality
Huygens' wave theory was less popular because
Newton powerful & influential
Light casts sharp shadows - light does not appear to diffract around objects
Light travels through a vacuum
even though beams of light could cross without interfering with each other.
Newton's particle theory of light said that
forces that are capable of repelling light particles act close to the surface of a material, at a normal to the surface
at a mirror surface the force repels light so that angle i = angle r
at an interface between two substances of different optical density, an attractive force accelerates particles entering the denser medium, so that they bend towards the normal
particles have fits of easy reflection and fits of easy transmission, so they can be both reflected and refracted.
different colours of particles are refracted more than others
It was disproved by
Young's double slit experiment
the discovery that light actually travels slower in glass
Fresnel, who proved that a very thin grating would be required for diffraction
Maxwell proposed that, since a changing magnetic field caused a changing electric field and vice versa, an EM wave consisting alternately of both could propagate through space. A B-field causes an E-field causes a B-field and so on.
He predicted the wave speed as c = 1 / Ö(m0e0). This gave a value close to the known value of c.
Discovered radio waves. Used a spark gap transmitter and a wire loop receiver to do this. The transmitter is effectively a high frequency resonator. The plates are charged by the induction coil, and the charge is dissipated through the resistance between the air gaps when the spark occurs. At this point, a high frequency a.c. current flows in the circuit. This resonance frequency is the same as the frequency of the EM waves emitted.
Hertz could only detect the waves when his receiver was pointing at them (don't know which way round that is) and thus found they were polarised as Maxwell had suggested. He also set up a standing wave and found the wavelength (distance between two nodes is half a wavelength).
Michelson 1926 (finding c accurately)
Rotating
octagonal prism on Mt. Wilson.
A black body absorbs all the radiation incident upon it. It is also a good radiator (good absorber = good emitter). The box with matt black insides comes close to this in practice. A black body emitter uses such a box. Since most of the radiation produced by the inside of the box is absorbed by other parts, the radiation output is a mixture of radiation from all over the inside of the box. There are no problems due to hot spots or cold spots.
Black body spectrum
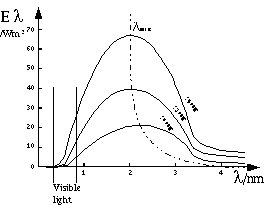Found using black body radiator, two concave mirrors, a slit and
fluorspar prism. The concave mirrors produce parallel or nearly-parallel
radiation. The prism splits the radiation up so that it can be measured using a
linear bolometer: strip of Pt foil, painted black. Resistance changes with
temperature, so a Wheatstone bridge is used to find the resistance and from it
the magnitude of radiation with a particular wavelength. You can get a radiation
spectrum for emissions from a black body at a particular temperature.
Wien's displacement law: lmax = constant
Stefan's law: Total energy radiated E = sT 4
s is Stefan's constant.
Classical physics could only explain black body radiation in terms of each part of the black body radiating energy of any wavelength. The Rayleigh-Jeans formula was based on classical physics and is correct for large l, but incorrectly tends to infinity for small l.
Planck found a correct formula from experimental results: Planck's radiation law. It was impossible to justify this in terms of classical physics. Planck concluded that the known laws of physics did not necessarily apply on an atomic scale. He proposed instead that energy can be absorbed or radiated only in discrete packets: quanta, each of energy hf. This was the beginning of the quantum theory, as it implies that the energy of a system can only change in discrete amounts.
h = Planck's constant
Boltzmann's constant, by the way, is the ratio R / L (L = Avogadro's number).
Einstein's photoelectric theory 1905
Lenard did some experiments around 1900 in which he researched the effect, which had been discovered by Hertz, and discovered a few things about it which could not be explained by the classical physics "wave theory" of light. This stated that light energy would be distributed equally to all the atoms on the surface, and therefore that electron emission should depend only on intensity. Einstein's theory was drawn up to explain why the photoelectric effect would not occur below a particular frequency of light, and why the e- emitted had a kinetic energy dependant on the light frequency.
hf = F + ½mv2
Millikan's experiment was a more careful test of the theory. Based on using an electric field to stop the photoelectrically emitted electrons. The p.d. was adjusted to find the point where it was just enough to stop the electrons. (work done by electron against a p.d. = energy lost by electron due to deceleration = eV). From this Millikan found the k.e. of the electrons and was able to plot a graph of light frequency against electron energy for a few metals (Li, K, Na). He also found the work function of these metals which turned out to be close to the one for thermionic emission, and found an accurate value of h.
Suggested that, as light could be considered as consisting of photons, each of energy hf, then matter might also have a wavelength.
For a photon:
E = hf and p = E/c
E = cp = hf therefore p = hf / c
But c / f = l. So p = h / l.
De Broglie's hypothesis was that a particle of momentum p will have wavelength l. This is now called the de Broglie wavelength.
From this, it follows that matter can be diffracted, and Davisson and Germer succeeded in diffracting electrons. Later experiments found that it was possible to diffract neutrons, protons, H and He atoms.
Davisson and Germer used a technique similar to that used for X-ray diffraction to look at electron diffraction patterns. They fired beams of electrons at Ni crystals- the beams were diffracted by the atoms. The pattern was analysed using a Faraday cylinder as a collector.
GP Thomson used very thin metal foils and a photographic plate to show electron diffraction. The polycrystalline (randomly structured) foil produced ring patterns- with the same wavelength predicted by de Broglie.
The wavelength of an electron is l = h /Ö(2meV)
(proved using
k.e. formulae for electrons, and p = mv = h / l
)
The waves do not really exist: except in terms of probability. The amplitude of a wave at a particular point in space is found by the wave function Y, where Y is a function of x, y, z and t. eg. amplitude = Y(x,y,z,t). The square of this amplitude is the probability of the particle being at this point, at this time.
The probability of a photon of light being at a particular point depends on the light intensity at that point, which depends on the amplitude of the electric field vector.
So a particle cannot be said to be at one particular point: the probability will be non-zero for a small region of space in all cases.
The TEM has a greater resolving power than the best theoretical optical microscope, because the de Broglie wavelength of the electrons it uses is less than the minimum wavelength of blue light. (Optical can resolve objects 2 x 10-7 m apart, electron can theoretically resolve objects 2 x 10-12 apart).
But...
electromagnetic lenses are not perfect- there is an effect similar to spherical aberration in an optical lens
electrons are emitted with a range of energies, and since the trajectory of an electron depends on it's speed (effect of lens) it may end up at different points on the image depending on it's initial kinetic energy. (like chromatic aberration)
specimen must be very thin so that the electrons have enough energy on leaving the specimen that there is still a reasonable resolution (not too much decrease in l)
slight variations in current in the electromagnetic lenses cause the image focus to suffer
Process: gun -> condenser -> object -> objective -> projector -> final image
The STM uses electron tunnelling. As an electron can be treated as a wave, there is a possibility of it being at any point around the point where it is most likely to be. It can even cross potential energy barriers if there is a possibility of it being on the other side. This allows electrons to jump the gap between the surface being investigated and the STM probe. The current is maintained by moving the probe up and down as the surface is scanned, to trace a map of surface.
this version 0.0.1 - was taken and adapted from a web search - I forget where I found it - but acknowledgements go to whoever.