
Scalars are quantities that have magnitude only:
Eg: Length, speed, mass, density, energy, power,
temperature, charge and pd
Vectors are quantities that have both direction and
magnitude:
Eg: Displacement,
force, torque, velocity, acceleration, momentum, electric current and electric
charge.
| O | A |
 |
B |
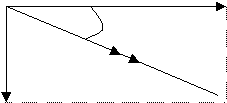
When we add two vectors their sum is called the resultant.
In the diagram OB = OA + AB
The two vectors can form 2 sides of a triangle
If the vector arrows follow on from one another (for addition) then the resultant is the third side of the triangle.
Parallelogram rule: it can be easier to make OA and AB two touching corners of a parallelogram. The resultant is the diagonal across the parallelogram. If done to scale this can be a good way to allow us to measure the magnitude (length) and direction (angle) of a resultant vector.
O 30o A
B
NB. Problems will only be given using vectors at right
angles – therefore calculation methods using trigonometry and Pythagoras are a
bit easier.
NB2. To subtract vectors – simply swap the direction of the subtracting vector and do the same as above.
Q1.
Consider two tug boats pulling a cruise liner out of a harbour.
Tugboat A is pulling with a force of 200kN N45oE. Tugboat B is
pulling with a force of 300kN S45oE.
a) Draw a scale diagrams showing the boats’ movement.
b) Calculate (or measure) the angle between the two tugboats.
c) Calculate the resultant force on the cruise liner – use pythogoras
d)
Calculate the direction the cruise ship is being pulled – use trig.
Q2.
Draw sketches to help add and then subtract the following vectors:
|
Vector 1 |
Vector 2 |
Addition
resultant |
Subtraction resultant |
|
20N South |
20N East |
|
|
|
5cm North |
7cm West |
|
|
|
40 m/s N50oE |
60m/s S40oE |
|
|
Q3
A ferry is crossing a river. Its
engines propel the boat with a velocity of 10m/s North. The river is moving with a current of 4m/s West.
Calculate the resultant velocity of the boat.
Make sure you draw a sketch to help.
Q4 and Q5 are from Breithaupt fourth edition – P.15 Q 1.9 and 1.10
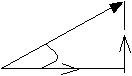
Forces are vector quantities; they have both size and direction.
Resolving a force
into its components means replacing the original force with two other forces
which would have added together to produce the same effect.
|
F |
|
 |
F1 |
|
F2 |
There are an infinite number of combinations of F1 and F2 which are equivalent to F but if ...
F1 and F2 are said to be components of F
They are chosen to be at right angles to each other so
that:
F12 + F22 = F2
In general :
| if force= F
and
angle=q |
 |
F1= F cos q |
| F2 = F sin q |
See P. 42 of Breithaupt – 4th ed.
Forces which act on objects but which do not cause an
acceleration are in equilibrium with each other. The study of forces which are
in equilibrium is called statics.
We need to be able to consider forces in two dimensions -
either when an object is at rest or when it is moving at a constant speed. In
both of these situations the forces are in equilibrium. To do this, we need to
be able to resolve forces.
The condition for equilibrium for three vector forces
acting at a point is:
This means that if the above relationship is true for the
forces – then we can say they are “in equilibrium”.
We can prove equilibrium in two ways – by scale
diagrams (3 forces must make a closed triangle) – or – by resolving all the
forces into horizontal and vertical components (they must all add to zero)
Statics is the
study of objects in equilibrium.
This picture is in
equilibrium.
T
T
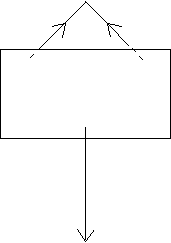
If the forces on the picture are redrawn nose to tail then it is possible to determine if there is a resultant force or if the picture is at equilibrium.
| T | 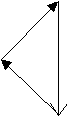 |
W |
| T |
|
R |
||
 |
3N | |
|
7N |
|
R2 = 32 + 72 R = Ö58 = 7.6N |
Angle between resultant and 7N force = q tan q = 3
7 q = 23° |
P. 42 Breithaupt – 4th ed. – with either:
spring balances – nailed and attached with string
OR
2 Weights hanging over pulleys attached to another
weight in between
Draw scale vector diagrams of the three forces and prove
that they are in equilibrium – first by using the closed triangle method and
then by resolving forces.
Notes on resolving forces method:
Imagine 3 forces see diagram -
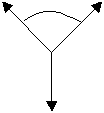 10N
10N
symmetrical
10N
10N
symmetrical
120o
10N
| half of 120o is angle to vertical | |
| Prove they are in equilibrium like this: | |
|
Vertical component of top two forces = 2 x 10 x cos 60o = 10N |
|
| Vertical component of lower force = -10N (assume convention up = positive) | |
| 10 + -10 = 0 therefore have vertical equilibrium | |
|
Horizontal component of right hand top force = -10 x sin 60o (assume a convention right is positive) Horizontal component of bottom force = Adding gives zero again – so horizontal equilibrium. QED
|
|
 |
Breithaupt – 4th Ed – P. 52 – Qns 3.1, 3.2, 3.3, 3.4, 3.5 - link to answer sheet
The moment of a force is a measure of it’s “turning effect”. These are required in situations when forces are rotating something – eg. Levers.
![]()
Distance = s force = F moment = Fs
Couple: these are when 2 equal but opposite forces are turning an object (ie when they act at different points on the object)
F

s F couple = Fs
The moment of a couple about any point = force x shortest distance between their lines of action
When a body is in equilibrium - the sum of the clockwise moments about any pivot must equal the sum of the anticlockwise moments about that pivot.
You
need notes on “Couple” and an example calculation. You need to indicate how it compares and contrasts with
“Moment”
Complete
your notes in this section with notes on “Torque”
The centre of mass (or the centre
of gravity) of a body is the point where its weight is considered to act.
You should be able to use the idea of the centre of mass of an object to decide if the object is stable or not. (Eg. Will it topple over or not?)
Read about how to estimate the position of the centre of mass (also known as the centre of gravity) of a regular laminate.
Borrow
a laminate and find it’s centre of mass.
Explain how the method works – referring to the principle of moments.
Breithaupt 4th Edn. P. 52
(see how far you can get – don’t labour it – move onto the next if TOO hard and come back if you have time – but ensure you leave PLENTY of time – some of these questions are VERY challenging and extend your skills to grade “A” and beyond)