A black body is
defined as an object which absorbs all wavelengths of radiation incident upon
it. It appears black because it reflects no light. If a surface is capable of
absorbing all wavelengths then it must also be capable of emitting all
wavelengths. So the radiation emitted by a black body contains all wavelengths.
An example of a black
body is a small hole in the door of a furnace. Any thermal radiation entering
the hole from outside passes into the furnace and is absorbed by the inside
walls. The inside walls are very hot and so they emit thermal radiation very
strongly ; some of this radiation may pass out through the small hole. The
emitted radiation from the small hole will contain all wavelengths.
Stars are also black
body radiators. Their surface temperature can be estimated by examining the
radiation they emit.
Black
body radiation from a source at constant temperature contains a continuous range
of wavelengths. However the energy carried by the radiation is not evenly
distributed across all the wavelengths and the distribution changes if the
temperature of the source changes. The proportion of the energy carried at the
shorter wavelengths increases as the temperature of the source increases.

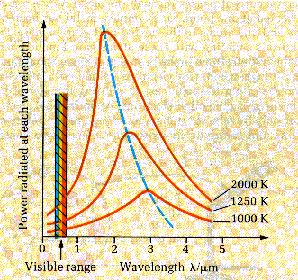
The graph shows how
the energy is distributed over the wavelength range for a given source
temperature. At each source temperature the curve has a peak showing that the
proportion of energy carried away is greatest for one particular wavelength.
This wavelength decreases as the temperature of the source increases according
to an equation called Wienís law,
![]()
where lp
= peak wavelength and T = source surface temperature.
The area under the curve gives the total radiated energy per unit surface area at that particular temperature. The link between radiated power from a black body radiator at constant temperature was established in 1884 and it is called Stefanís law
![]()
where Q/t = energy/second radiated away
A = surface area
T = surface temperature (K)
s = Stefanís constant
The black body
radiation curves (previous diagram) were produced as a result of detailed
research by two scientists, Lummer and Pringsheim, in the late 19th
century. Maxwellís wave theory could successfully predict the shape of these
curves at either side of the peak but it predicted a peak of infinite height.
This problem was called the ultraviolet catastrophe because the infinitely high
peak occurred at a wavelength in the UV part of the spectrum.
The
problem was eventually solved by Planck and Einstein who established the idea of
photons with discrete or quantised energy values. Black body radiation curves
are completely explained by the ideas of the photon theory.
The failure of the classical wave theory to explain black body radiation curves caused a major rethink of the nature of light and in 1900 Max Planck suggested that energy was not generated continuously but in packets called quanta. These packets of energy have a value given by
![]()
where E = energy
h = Planckís constant
f = frequency of emitted radiation
Each quantum can have a certain energy value and there are no values in between these. On a large scale this fact would not be obvious because Planckís constant is very small making the individual energies much less than the energy of the system. This would make the energy of the system appear to be continuous in nature.
On an atomic scale this idea is extremely important and Planckís radiation law is a result of his work
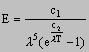
where E = height of peak on black body radiation curve
c1, c2 = constants
l = wavelength
Planckís radiation law fits the experimental results exactly.
Planckís ideas on quantum theory represent one of the major advances in scientific thinking in the history of science.
It is not easy to understand why Planck's quantisation of energy helped solve the UV catastrophe - this link might help - beware - it's very un-mathematical