More legacy questions - with some mark schemes
click here to jump to: summer97, spring97, summer96, spring96, summer95, spring95
PH02
Summer 97
view
mark scheme
1 The isotope of 238 92 U is at the head of a chain of radioactive decays. The first few decays in the series are shown below.
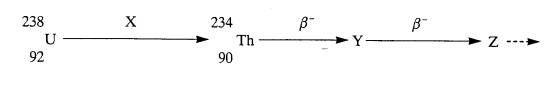
(a) Use data from the data book to identify the decay process X and the decay products Y and Z.
(3)
(b) (i) Calculate the mass difference between U-238 and Th-234.
(ii) Show that the energy released in this decay is about 4 MeV.
(4)=(7)
3

A trolley of mass 0.40 kg is attached to two fixed points by springs as shown. When it is displaced horizontally 0.20 m from its equilibrium position and released, it moves with simple harmonic motion with a period of 4.0 s.
(a) Ignoring any frictional effects, calculate
(i) the maximum speed of the trolley,
(ii) the maximum kinetic energy of the trolley,
(iii) the effective stiffness constant, k, of the spring system.
(5)
(b) In practice, frictional forces gradually reduce the kinetic energy of the trolley. If the trolley loses one-tenth of its kinetic energy in every complete oscillation, calculate the kinetic energy of the trolley at the equilibrium position when it has made four complete oscillations. Assume that the kinetic energy when it first passes the equilibrium position is the value which you have calculated in (a) (ii).
(2)=(7)
4 (a)
Explain the meanings of the following terms:
free vibration
forced vibration
resonance
(3)
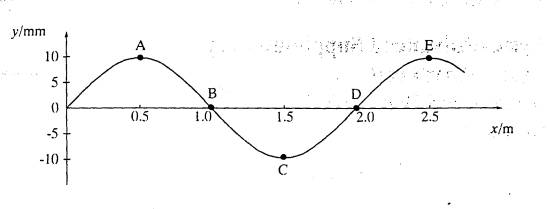
(b)

A, B and C are three pendulums, each with a light paper cone for a bob. X is another pendulum with a heavy metal bob. Pendulum X is displaced perpendicular to the plane containing the bobs at rest and then released.
Compare the motions of pendulums A, B and C to that of X, with reference to period and amplitude.
Pendulum A:
Pendulum B:
Pendulum C
(3)=(6)
5 (a)
Explain what is
meant by
(i) unpolarised light
(ii) plane polarised light
(2)
(b)
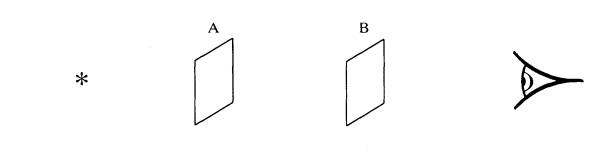
A light source appears bright when viewed through two pieces of polaroid, as shown. Describe what is seen when B is slowly rotated through 180o in its own plane.
(2)
(c) (i) Tick which of the following categories of waves can be polarised.

(ii) State your criterion for deciding which to tick.
.(2)=(6)
6 (a) Describe, with the aid of a diagram, how you would set up the apparatus to produce and observe optical interference fringes using a double slit and any other essential apparatus.
(3)
(b) A student set up a two-slit interference experiment in the laboratory to determine the wavelength of the yellow light from a sodium lamp. A travelling microscope was used to make measurements on the fringes produced and the readings obtained are shown below. The slit separation was 0.40 mm and the distance from the double slit to the plane in which the fringes were viewed was 1.80 m.

Use these values to calculate the wavelength of the yellow light.
(4)
(c) For the apparatus used in (b), describe and explain the effect on the appearance of the fringes of
(i) reducing the separation of the double slits but keeping the width of each slit constant,
(ii) making each of the double slits wider but keeping the slit separation constant.
(4)
(d) You have been asked to demonstrate two-source interference with sound waves. Describe, with the aid of a diagram which shows the approximate distances involved, how you would do this.
. . (4)=(15)
3 Describe an experiment you would perform, using the same apparatus in each case, to illustrate the meaning of each of the following terms. In each case explain what you would observe.
(i) free vibrations
(ii) forced vibrations
(iii) resonance
. . (6)=(6)
5
(a)
Explain why the apertures (or lines) of a diffraction grating for
visible light should be
(i) narrow
compared to the wavelength of visible light,
(ii) close together,
(iii) equally spaced.
(3)
(b)
Sodium light of wavelength 589 nm falls normally on a diffraction
grating which has 600 lines per mm. Calculate the angle between the directions
in which the first order and second order maxima, on the same side of the
straight through position,
are observed.
(5)=(8)
PH02 June 1996
view mark scheme
1
Red light of wavelength 7.00 x 10-7 rn, incident normally on
a diffraction grating, gave a first order maximum at an angle of 75o.
(a) Calculate the
spacing of the diffraction grating.
(b) Calculate the angle at
which the first order maximum for violet light of wavelength 4.50 x 10-7 m
would be observed.
(c) At what angle or angles
would a detector receive radiation which is of wavelength 7.5 x 10-7
m transmitted by the grating? Explain your answer.
(2)=(4)
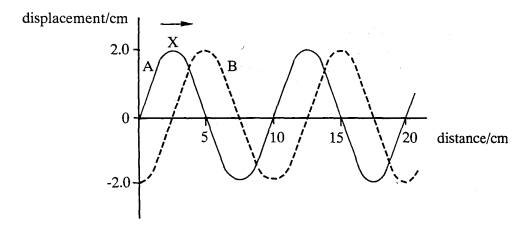
4. (b) Graph C below shows the variation of displacement with distance along a stationary transverse wave at time
t = 0 when the displacement of the particles is the greatest. The period of the vibrations causing the wave is 0.10 s.
(i) Draw, on the same axes, the appearance of the wave at t = 0.025 s, labelling this graph D, and the appearance of the wave at t = 0.050 s, labelling this graph E.
(ii) Compare the frequency, amplitude and phase of the particles whose positions at t = 0 are shown by V, W and Z.
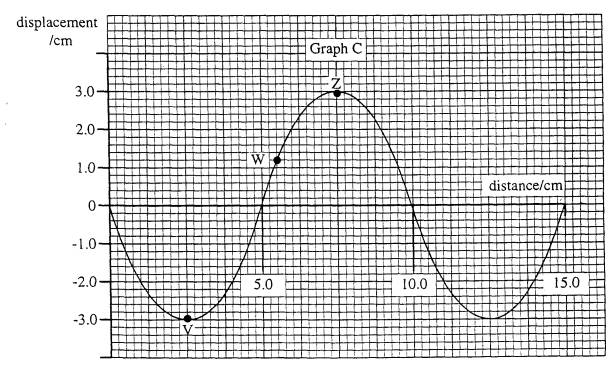
(iii) State the two conditions necessary for the production of a stationary wave.
(8)