|
"Legacy" questions - mainly from old PH02 module |
jump to: June2001, Feb2001, June200, Merch2000, June99(PH06), June99, March99, June98, March98
3 (a) Define simple harmonic motion.
(2)
(b) State where the magnitude of the acceleration is greatest during simple harmonic motion.
(c) The velocity of a mass, m, undergoing simple harmonic motion is given by
![]()
where w is the angular frequency, and xo and x represent displacements of the mass from its equilibrium position.
(i) What is xo?
(ii) Give an expression for the kinetic energy of the mass, in terms of m, w x and xo, when the displacement is x.
(iii) Sketch, on the axes, how the velocity of the mass varies with displacement.
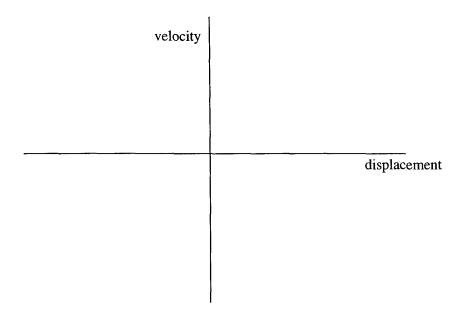
(4)=(7)
4 The diagram below is a full-size reproduction of the interference fringes produced when red light of wavelength 633nnm from a laser passes through a double slit on to a screen which is 2.5m from the double slit.
![]()
(a) By making measurements on the fringe pattern as accurately as possible, and by using the above data, determine the separation of the double slit.
(4)
(b) State and explain how the fringe pattern would change if a source of monochromatic green light were substituted for the red one.
(2)
(c) Using an appropriate arrangement and the same double slit, fringes are produced using white light. The central fringe is white and the other fringes are coloured. Explain why the central fringe is white.
(2)=(8)
6. Polaroid sunglasses are often sold with a small additional piece of polaroid attached to them.
(a) Describe a simple experiment which you can carry out using this piece of material to show that the sunglasses are also made from polaroid material.
(b) Polarisation of light waves suggests one fact about the nature of light waves. What is this fact?
2 (a) Figure 1 shows the undisturbed positions of the vibrating parts of a transverse wave machine. When the machine is working it produces progressive waves travelling from left to right. Figure 2 shows the wave on the machine at a particular time.
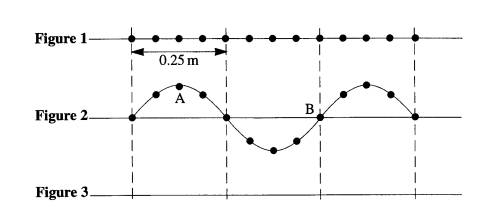
The source frequency is 0.40 Hz.
(i) Explain how you know from the diagram that the wave is transverse.
(ii) Compare the motions of particles A and B with respect to their frequency, amplitude and phase.
frequency
amplitude
phase .............................................................................................................................
(iii) Calculate
the period of the wave and on Figure 3 sketch the position of the wave
1.25 s later than in Figure 2.
(7)
(b) Figure 4 shows a stationary wave formed on a vibrating string fixed at one end. The frequency of vibration is such that the string vibrates in two loops.
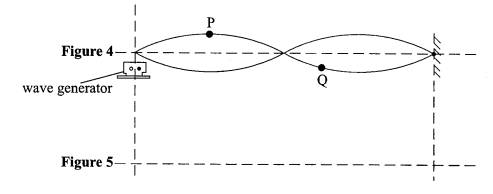
(i) Explain how the stationary wave is formed on the string.
(ii) Compare the motion of points P and Q with respect to their frequency, amplitude and phase.
frequency
amplitude
phase
(iii) Sketch on Figure 5 the appearance of the string when the frequency is doubled.
Explain your answer. Show on your diagram three points R, S and T which are in phase.
(8)=(15)
3 In a fairground shooting gallery, a duck target oscillates along line BC with simple harmonic motion about point A. The amplitude of the motion is 0.50 m and the time period is 4.0s.

(a) Calculate the maximum speed of the duck.
(2 marks)
(b) A competitor in the shooting gallery has to hit the centre of the duck to score points. In which positions of the duck would the competitor have the best chance of hitting it? Explain your answer. (2 marks)
(c) Sketch a velocity-time graph for the motion during the time in which the duck moves from A to B and back to A.
(3 marks)
4 The diagrams show water waves in a ripple tank incident normally on a slit. The depth of the water in the tank is the same at all points.

(a) On the diagram above sketch the appearance of the waves after passing through the slit, showing the direction(s) of propagation and the wavelengths of the waves. (2 marks)
(b) The width of the slit is reduced until the slit is about the same size as the wavelength of the water waves. On the diagram below, show the waves after they have passed through the slit.
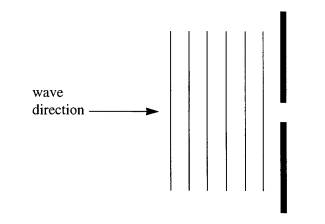
(1 mark)
(c) Name the phenomenon which takes place in parts (a) and (b).
(1 mark)=4
5
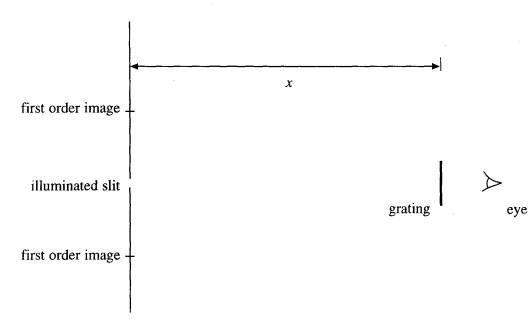
A student observes diffracted images of an illuminated slit source produced by a diffraction grating. First and second order images are seen in the plane of the slit. The first order images are 0.20 m either side of the centre of the slit. The wavelength of the light is 589 nm and the grating has 5.0 X 105 rulings per metre.
(a) (i) Show that the angle at which the first order appears in approximately 17o
(ii) Calculate the value of x, the distance between the grating and the slit.
(4 marks)
(b) Show whether or not the second order images will be positioned less than 0.50m from the centre of the slit.
(2 marks)
5 (a) (i) Complete the equation below which represents the induced fission of a nucleus of uranium
![]()
![]()
(ii) The graph shows the binding energy per nucleon plotted against nucleon number A.
Mark on the graph the position of each of the three nuclei in the equation.

(iii) Hence determine the energy released in the fission process represented by the equation.
(6)
(b) (i) Use your answer to part (a)(iii) to estimate the energy released when 1.0kg of uranium, containing 3% by mass of 235 U, undergoes fission.
(ii) Oil releases approximately 50 W of heat per kg when it is burned in air. State and explain one advantage and one disadvantage of using nuclear fuel to produce electricity.
(6)=(12)
2 A spring, which obeys Hooke's law, hangs vertically from a fixed support and requires a force of 2.0 N to produce an extension of 50 mm. A mass of 0.50 kg is attached to the lower end of the spring. The mass is pulled down a distance of 20 mm from the equilibrium position and then released.
(a) (i) Show that the time period of the simple harmonic vibrations is 0.70s.
(ii) Sketch the displacement of the mass against time, starting from the moment of release and continuing for two oscillations. Show appropriate time and distance scales on the axes.
(5)

(b) The mass-spring system described in part (a) is attached to a support which can be made to vibrate vertically with a small amplitude. Describe the motion of the mass‑spring system with reference to frequency and amplitude when the support is driven at a frequency of
(i) 0.5 Hz,
(ii) 1.4 Hz.
(3)
3 (a) A double slit interference experiment is set up in a laboratory using a source of yellow monochromatic light of wavelength 5.86 x 10‑7 m. The separation of the two vertical. parallel slits is 0.36mm and the distance from the slits to the plane where the fringes are observed is 1.80 m.
(i) Describe the appearance of the fringes.
(ii) Calculate the fringe separation, and also the angle between the middle of the central fringe and the middle of the second bright fringe.
(iii) Explain why more fringes will be seen if each of the slits is made narrower, assuming that no other changes are made.
(8)
(b) Light of wavelength 5.86 x 10-7 m falls at right angles on a diffraction grating which has 400 lines per mm.
(i) Calculate the angle between the straight through image and the first order image.
(ii) Determine the highest order image, which can be seen with this arrangement.
(5)
(c) Give two reasons why the diffraction grating arrangement is more suitable for the accurate measurement of the wavelength of light than the two-slit interference arrangement.
(2)
4 Stationary waves in air can be demonstrated using a long horizontal tube which contains fine powder. With a loudspeaker connected to a signal generator positioned at one end of the tube, stationary waves are formed by reflection of waves from the ends of the tube. The diagram shows part of the tube in such an arrangement. The powder forms heaps at nodes.
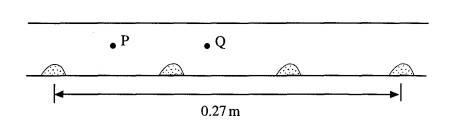
speed of sound waves in air = 340 m s-1
(a) Determine
(i) the wavelength of the waves,
(ii) the frequency of vibration of the loudspeaker.
(2)
(b) Distinguish between longitudinal waves and transverse waves and state which type of wave is being generated in the tube.
(3)
(c) P and Q are two points in the tube. Compare the motion of air particles at P with the motion of air particles at Q with reference to
(i) frequency,
(ii) amplitude,
(iii) phase.
(3)
1 (a) For a sound wave travelling through air, explain what is meant by particle displacement, amplitude and wavelength.
(4)
(b)
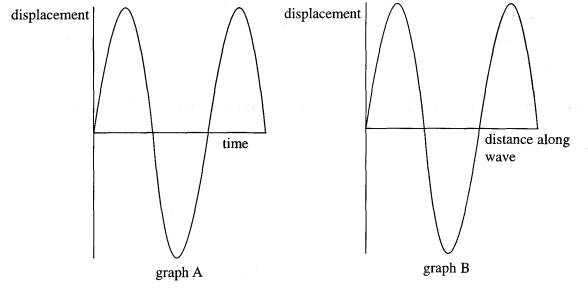
Graph A shows the variation of particle displacement with time at a point on the path of a progressive wave of constant amplitude. Graph B shows the variation of particle displacement with distance along the same wave at a particular instant.
(i) Show on graph A
(1) the wave amplitude, A,
(2) the period, T, of the vibrations providing the wave.
(ii) Show on graph B
(1) the wavelength of the wave, l,
(2) two points, P and Q, which are always p/2 out of phase. (4)
(8)
2 (a) Explain what is meant by the binding energy of a nucleus.
(2)
(b) Using data from the Data booklet, calculate the binding energy, in MeV of a nucleus of 5 Li
(5)
3
(a) A
vibrating system which is experiencing forced
vibrations may show resonance.
Explain what is meant by
forced vibrations
resonance
(3)
(b) (i)
Explain what is meant by damping.
(ii) What effect does damping have on resonance?
(2)
4 (a) A helium-neon laser produces monochromatic light of wavelength 632.8 nm which falls normally on a diffraction grating. A first order maximum is produced at an angle of 18.5o measured from the normal to the grating.
Calculate
(i) the number of lines per metre on the grating,
(ii) the highest order which is observable.
(6)
(b) When the grating is used with a different monochromatic source, the first order maximum is observed at an angle of 17.2o
Calculate the wavelength of this second source.
(2)
2 (a) Nuclear fission can occur when a neutron is absorbed by a nucleus of uranium‑235. An incomplete equation for a typical fission reaction is given below.
![]()
(i) State the nuclear composition of X.
proton number ..................................................................................................................
neutron number ................................................................................................................
(ii) Name the element of which X is an isotope.
(3)
(b) In a small nuclear power plant one fifth of the fission energy is converted into a useful output power of 10 MW. If the average energy released per fission is 3.2 x 10 –11 J, calculate the number of uranium-235 nuclei, which will undergo fission per day.
(3)
3 (a)
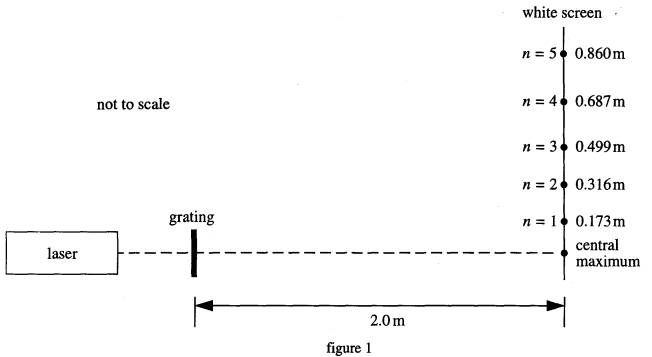
In a laboratory experiment, monochromatic light of wavelength 633 nm from a laser is incident normal to a diffraction grating. The diffracted waves are received on a white screen, which is parallel to the plane of the grating and 2.0 m from it. Figure 1 shows the positions of the diffraction maxima with distances measured from the central maximum.
By means of a graphical method, use all these measurements to determine a mean value for the number of rulings per unit length of the grating.
(6)
 (b) Describe
and explain the effect, if any, on the appearance of the diffraction pattern of
(b) Describe
and explain the effect, if any, on the appearance of the diffraction pattern of
(i) using a grating which has more rulings per unit length,
(ii) using a laser source which has a shorter wavelength,
(iii) increasing the distance between the grating and the screen.
(6)
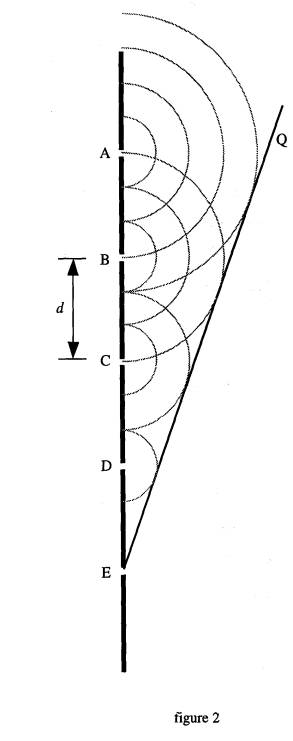
(c) Figure 2, opposite, shows the diffracted waves from four narrow slits of a diffraction grating similar to the one described in part (a). The slit separation
AB = BC = CD = DE = d and EQ is a line drawn at a tangent to several wavefronts and which makes an angle q with the grating.
(i) Explain why the waves advancing perpendicular to EQ will reinforce if superposed.
(ii) Show
that this will happen when sin q
= l/2
(3)
5. The diagram shows two
identical loudspeakers, A and B, placed 0.75 m apart. Each loudspeaker emits
sound of frequency 2000 Hz.
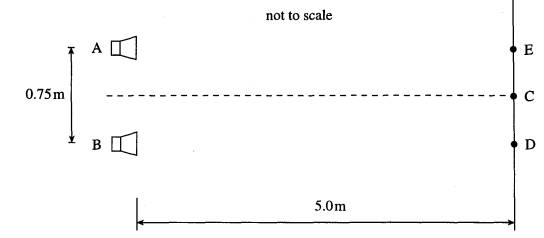
Point C is on a line midway between the speakers and 5.0 m away from the line joining the A listener at C hears a maximum intensity of sound. If the listener then moves from C to E or D, the sound intensity heard decreases to a minimum. Further movement in the same direction results in the repeated increase and decrease in the sound intensity.
speed of sound in air = 330 m s-1
(a) Explain why the sound intensity
(i) is a maximum at Q
(ii) is a minimum at D or E.
(4)
(b) Calculate
(i) the wavelength of the sound,
(ii) the
distance CE.
(4)
1. Nuclei of
218 Po decay by the emission of an alpha particle
to form a stable isotope of an element X.
84
You may assume that no gamma emission accompanies the decay.
(a) (i)
State the proton number and the nucleon number of X.
(ii) Identify
the element X. (use data book)
(2)
(b) Each decaying nucleus of Po releases 8.6 x 10-13 J of energy.
(i) State the form in which this energy initially appears.
(ii) Using only the information provided in the question, calculate the difference in mass between the original 218 Po atom and the combined mass of an atom of X and an alpha particle.
speed of light in vacuum = 3.0 x 108 ms-1
(3)=(5)
4 Explain the differences between (a) an undamped progressive transverse wave and (b) a stationary transverse wave, in terms of (i) amplitude, (ii) phase and (iii) energy transfer.
(5)
5. The diagram for this question is drawn to scale and 1 mm on the diagram represents an actual distance of 5 mm.

S1 and S2 are identical coherent transmitters emitting, in phase, microwaves with a wavelength of 25 mm. They are positioned 250 mm apart on a horizontal surface and a detector can be placed anywhere along the line YY' which is in the same plane as the transmitters and parallel to the line containing S1 and S2.
(a) Explain
what is meant by coherent.
(2)
(b) By making measurements on the diagram and using the scale, determine the number of wavelengths in the path
(i) S1R,
(ii) S2R.
(iii) Use your answers to (i) and (ii) to determine whether or not you expect the signal received by a detector placed at R to be a maximum. Explain your answer.
(5)
(c) Describe how you would expect the signal strength to vary as the detector is moved from R to P via Q.
(2)
(d) Calculate the frequency of the microwaves.
(1)=(10)
PH02 June 1998 Click
here to view mark scheme
3 (a) Graph A shows the displacement at time t= 0 at different points on a progressive wave. Graph B shows the situation at t= 0.10s.
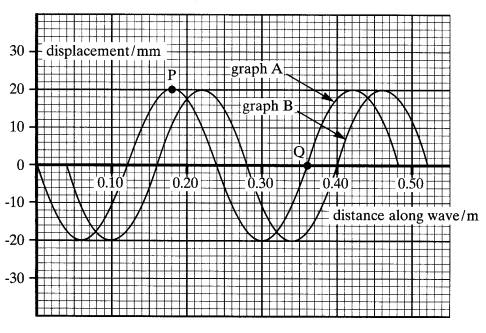
Use graphs A and B to determine, for the wave,
(i) the wavelength
(ii) the amplitude
(iii) the wave speed
(iv) the frequency of the wave
(v) the phase difference between points P and Q marked on graph A.
(6)
(b) Using the grid below, sketch a graph to show the variation with time of the displacement of point P on the graph in part (a), showing numerical scales on both axes.

(3)
(c) When a stone is thrown into a still pond, circular ripples spread out. How could you tell, from observations of the ripples, whether or not they were travelling at constant speed? Explain your answer.
(2)
(d) Describe an experiment to demonstrate that light waves are transverse.
(4)=(15)
4 (a) A student carried out an experiment to determine the grating spacing, d, of a diffraction grating by determining the diffraction angle in the second order for several spectral lines of known wavelength. These results are given in the table.
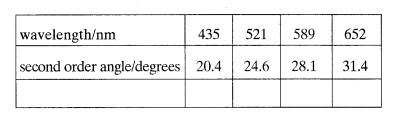
Use these results to obtain the values needed to plot a straight line
graph. Draw the graph onto A4 graph paper and use it to determine a value for d.
(6)
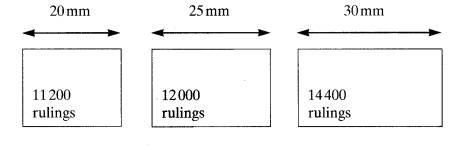
(b) Three diffraction gratings, illustrated below, are available for observing line spectra. The grating width and the total number of vertical rulings on the grating are given for each one. Determine which of the three gratings will give the largest diffraction angle in the first order with a given spectral line.
(3)
7 The diagram shows two small loudspeakers positioned a few metres apart with a small microphone, M, connected to an oscilloscope, positioned exactly midway between them. The loudspeakers are connected in parallel to a signal generator producing oscillations at a frequency of 3300Hz.
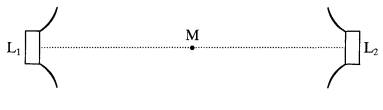
(a) Calculate the wavelength of the sound waves produced.
speed of sound waves in air 330 m
(1)
(b) The microphone is now moved slowly to the right.
(i) Describe and explain how the trace height on the oscilloscope will change as the position of the microphone is changed.
(ii) Explain why this occurs.
(4)=(5)
2
Use data from the Data booklet in this question.
(a) Give an equation for each of the following decay processes. State in each case the number of neutrons and the number of protons in the daughter nucleus.
(i) 15
C emits a beta- particle
6
(ii) 230 Th emits
an alpha particle.
90
(4)
(b) Calculate the energy, in MeV, which is released in the decay process in part (a) (ii).
(3)=(7)
3 (a) (i) Describe and explain, with the aid of a labelled diagram, the double slit arrangement which you would set up in order to produce and observe Young's interference fringes using monochromatic light.
(ii) Suggest approximate values for the slit separation and the distance from slits to screen.
slit separation
distance from slit to screen.
(6)
(b) (i) Describe two features of the interference fringes.
(ii) Describe and explain one change in the appearance of the fringes if the slit separation is reduced.
(4)
(c) (i) State the measurements you would make in order to determine the wavelength of the light used.
(ii) Calculate the fringe separation which would result, using the approximate values which you gave in part (a) (ii), assuming that the wavelength of light used is 600 nm.
(4)=(14)
4 (a)

The diagram shows a plan view of part of a diffraction grating of spacing d. Plane monochromatic waves of wavelength l are incident normally on the diffraction grating. The diffracted waves make an angle q with the normal. Derive from first principles the diffraction equation
![]()
(You may draw on the diagram if it assists your derivation.)
(4)
(b) A diffraction grating is illuminated with light of wavelength 577 nm. The second order maximum is formed at an angle of 41.25o to the normal. Calculate the total number of lines on the grating if it is 30mm wide.
(3)=(7)