|
Intensity |
|
 |
|
|
Position on screen |
Often quoted as a demonstration of the wave nature of light. It uses a single slit followed by a double slit to produce “fringes”. These are areas of light and dark caused by constructive and destructive interference.
Formula:
l
= ws
/ D
l
= wavelength of light,
w
= fringe width (centre to centre)
s
= slit spacing
D
= distance of screen from the double slits.
Note:
The use of the double slit is so that we have two sources that are coherent.
This means that the two sets of light waves are emitted with a constant
phase difference. As a result
the fringes stay in fixed positions.
Questions
are often set on the effect of altering the various variables in the equation.
E.g. a greater wavelength of light would result in wider fringes as l
is proportional to w
(for fixed s and D).
Important
to remember that red light has a greater wavelength than violet, so passing
white light through the double slit arrangement would result in a dispersion
of the coloured spectrum – with the red fringes showing greatest spacing.
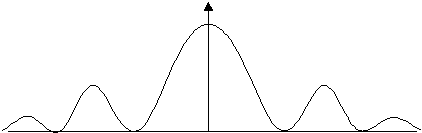
Fringes are also seen when a point source of light is viewed through a narrow single slit. In this case the fringes fade away from the central bright maximum. The central fringe is twice the width of the other fringes.
The narrower the slit the greater the diffraction.
The longer the wavelength the greater the diffraction.
|
Intensity |
|
 |
|
|
Position on screen |
Diffraction is when a wave passes through a narrow opening and is bent. Maximum diffraction occurs when the wavelength of the wave most closely matches the width of the gap.
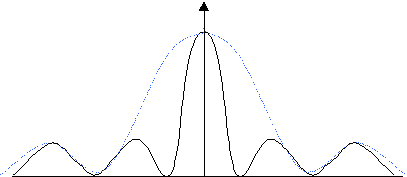
Note the brightness of Young’s double slit arrangement fades out at the edges two – this is due to the first single slit superimposing a single slit diffraction pattern on top of the double slit fringes.
In this example the dotted line represents the original single slit diffraction pattern. The unbroken line represents the double slit pattern as modulated by the single slit pattern.
|
Intensity |
|
 |
|
|
Position on screen |
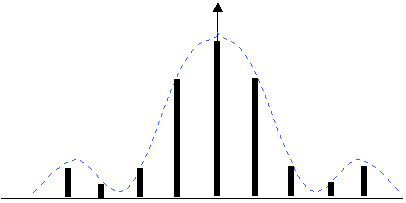
A plate with many closely spaced is called a diffraction grating. If there are many closely spaced slits then fewer but sharper fringes are seen. This is because each of the many slits transmit light but they cancel one another out in most directions. Each slit produces a diffracted set of waves but they reinforce each other only in certain directions.
The closer the slits, the more widely spaced are the
diffracted beams.
The longer the wavelength the more widely spaced are the
diffracted beams
White light gives a mini-spectrum of colours in each
diffracted beam.
Formula:
nl = d sin q
n
= order number of the beam
l = wavelength
d = slit spacing
q =
angle of diffraction of the nth order
This
needs to be derived:
Consider two slits on the grating (Q and P)
in close up and follow two paths of diffracted light from the two slits.
| Q
P
|
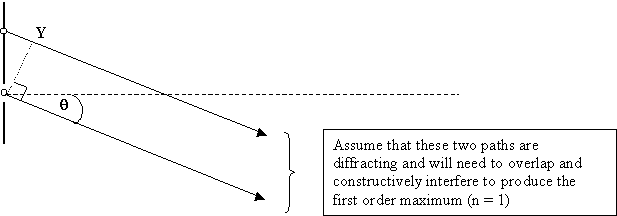 |
To understand this derivation you have to be confident of two facts.
1.
The angle of diffraction of the waves (q) is
equal to the angle QPY. Go
double check this fact and make sure you are confident of it.
2. The path difference between the two paths is equal to length QY. Again battle with this one until you are confident.
From trigonometry sin q = opposite / hypotenuse = sin [angle QPY] = QY / PQ (using fact number 1)
For constructive interference, the path difference must be equal to nl (so the waves arrive in phase with each other)
Or put another way path difference = QY = nl - for constructive interference (using fact number 2)
Put these two ideas tighter and:
sin q =
QY / PQ = nl
/ d
(where PQ = the slit spacing, d)
OR:
sin q = nl
/ d rearranges to give: nl
= d sin q
Grating
diffraction pattern:
see
diagram – for effect of single slit diffraction
 |
|
|
Position on screen |